Deformation export field definitions

Q&A
1

Hi All,

I have been working with deformation data exported from GPlates and I was just wondering if someone could point me to some “simple” definitions of the different fields which are exported - namely:

DilatationStrain, DilatationStrainRate, TotalStrainRate, and CrustalThinningFactor.

Is there any documentation which lists exactly what these parameters mean and how they are derived?

Cheers,
Tom

2

Hi Thomas,

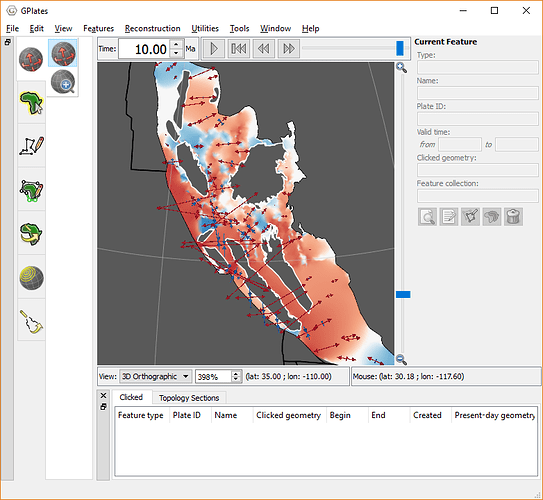
Starting with the easiest, CrustalThinningFactor, this is probably best described in the screenshot below…

image
image782×720 46.4 KB

And for the strain/strain-rate quantities:

  • DilatationStrain
    The strain dilatation is essentially the expansion or contraction of material (crust) defined as the change in volume divided by volume (and so is dimensionless, has no units). So this is a single scalar value that’s positive for extension and negative for contraction. For crustal extension we consider 2D (instead of a 3D volume), so the crust thins along the depth dimension and stretches along the surface 2D dimensions (eg, lat/lon). That surface strain is represented by a 2D tensor to capture the various types of strain (such as normal and shear strains) in the 2D surface dimensions. The dilatation then reduces these 2x2=4 tensor values to a single scalar which captures whether the crust expands or contracts overall (in 2D), at the particular surface point in question. And each surface point will have its own time-history of 2D strain tensors (and hence dilatations).
  • DilatationStrainRate
    This is similar to dilatation strain but is the time rate of change in volume divided by volume (and so has units of 1/second). Again, in our case, it’s 2D (not 3D) with the missing 1D coming from crustal thinning/thickening, which is why crustal thinning is dependent on dilatation strain rate.
  • TotalStrainRate
    This is actually the second invariant of the strain rate tensor but we (and others) call it total strain rate because it’s essentially a measure of all strain rate components (normal and shear strains) summed up. Similarly to dilatation strain rate this is another way to reduce the 2D tensor to a single scalar. There are different definitions of the second invariant, we use sqrt(trace(D^2)) where D is the symmetric form of the 2D velocity spatial gradient tensor. Taking the square of D (ie, D^2) means we capture the off-diagonal components of D which are the shears (trace is the sum of diagonal components). For comparison, dilatation strain rate is trace(D) which does not capture the off-diagonal shear components of D. This makes sense because dilatation rate is only interested in volume (or area) expansion and shear does not change the volume (under infinitesimal deformation).

There’s also principal strain which is where the 2D coordinate axes are rotated to the 2D principal axes where there is no longer any shear strain (the strain tensor becomes diagonal), so you just have compression/extension strain along the principal axes. GPlates exports this as the rotation angle to get to the major principal axis and the strain along the major and minor principal axes. You can also see this on the globe in GPlates if you select Show strain accululation when reconstructing using topologies…

image
image787×720 43.3 KB

image
image782×720 146 KB

The GPlates source code documents how each of these quantities are derived. Just look for the big comments that detail all the mathematics…

src/app-logic/DeformationStrainRate.h - derivation of strain rate dilatation and total strain rate (2nd invariant)
src/app-logic/DeformationStrain.h - derivation of strain dilatation
src/app-logic/DeformationStrain.cc - derivation of strain principal components, and accumulation of strain over time (due to strain rate)

These derivations are mostly based on two books: Introduction To The Mechanics Of A Continuous Medium by Malvern, and Continuum mechanics for engineers by Mase. Each of those books contains a chapter on strain and deformation, but also an earlier chapter on the essential mathematics, such as tensors, which is helpful since a lot of the derivations in the above-mentioned source files are based on tensors. However this is only useful if you really want to understand the derivations, because it does require an investment in time. If you just want a simple intuitive understanding of the quantities you mentioned it is unnecessary and, in my opinion, not recommended since it gets a bit involved :face_with_raised_eyebrow:

Regards,
John

3

Thank you, John! I always forget how useful those help buttons are in GPlates.

You will be high up on my thesis acknowledgements list at this rate.

Tom