Hi,
GPlates allows the user to retrieve the deformation field and a number of scalar values describing strain for deforming networks. My understanding of the algorithm behind this is the following:
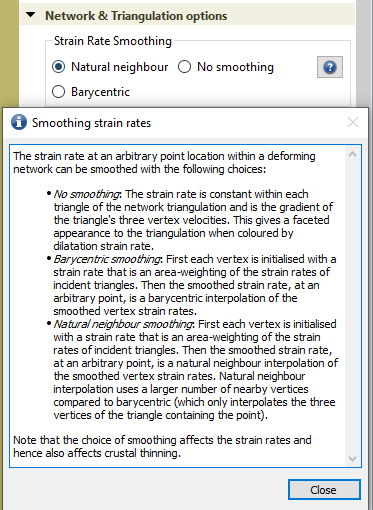
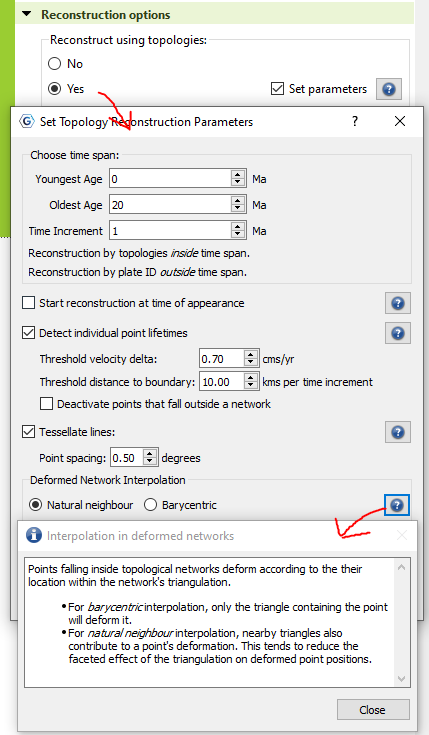
Firstly, it seems the strain rate is calculated for a triangular element. The triangulation of the mesh is updated at every timestep. For advecting Lagrangian markers, their location in the next time step (whether forward or backward in time) is then calculated using the relative coordinates in the triangular element (i.e. a shape function in for finite element methods).
My questions are the following:
-
I can generate a velocity field on a set of Eulerian points for any reference frame. Are these velocities calculated by simply using the vector distance between the current and projected location of these Eulerian points in the adjacent timesteps (depending on the choice of T, T+dt, T-dt, T or T-1/2dt, T+1/2dt as time interval for which the velocity is determined) divided by the time interval dt?
-
GPlates exports information on strain as a scalar value attached to a Lagrangian marker. This means means that the obtained strain fields is asymmetric in time, i.e when going from 100 to 0 Ma or from 0 to 100 Ma, I obtain two different sets of strain fields. In my reconstruction, this leads to either large gaps or between markers (going backwards in time) or a huge pile of markers in one place (going forward in time). Eulerian fields on the other hand are in principle symmetric in time. Is it also possible to export the strain fields for a set of Eulerian points?
Many thanks!
Thomas